By Eric Vandenbroeck and co-workers

The logic of human nature and causal networks

In addition to our earlier comment, John Mark Bishop recently wrote Artificial Intelligence is stupid and causal reasoning will not fix it. So the question is why.

As ear correlation means that there is a relationship, or pattern, between two different variables, but it does not tell us the nature of the relationship between them. In contrast, causation implies that beyond there being a relationship between two events, one event causes another event to occur.

As early on explained by Thomas Sowell, the concept of causation and its contrast with mere correlation is the lifeblood of science. What causes cancer? Or climate change? Or schizophrenia? It is woven into our everyday language, reasoning, and humor. The semantic contrast between “The ship sank” and “The ship was sunk” is whether the speaker asserts that there was a causal agent behind the event rather than a spontaneous occurrence. We appeal to causality whenever we ponder what to do about a leak, a draft, an ache or a pain. 

What Is Correlation? A correlation is a dependence of the value of one variable on the importance of another: if you know one, you can predict the other, at least approximately. (“Predict” here means “guess,” not “foretell”; you can expect the height of parents from the heights of their children or vice versa.

In 2020 Jeff Bezos claimed, All of my best decisions in business and life have been made with heart, intuition, gut, not analysis, implying that heart and guts lead to better decisions than analysis. But he did not tell us whether all of his worst decisions in business and life were also made with heart, intuition, and guts, nor whether the good gut decisions and bad analytic ones outnumbered the bad gut decisions and good analytic ones.

Illusory correlation, as this fallacy is called, was first demonstrated in a famous set of experiments by the psychologists Loren and Jean Chapman, who wondered why so many psychotherapists still used the Rorschach inkblot and Draw-a-Person tests even though every study that had ever tried to validate them showed no correlation between responses on the tests and psychological symptoms. The experimenters mischievously paired written descriptions of psychiatric patients with their reactions on the Draw-a-Person test, but in fact, the descriptions were fake and the pairings were random. They then asked a sample of students to report any patterns they saw across the pairs. The students, guided by their stereotypes, incorrectly estimated that hyper-masculine patients sketched more broad-shouldered men. More wide-eyed ones came from hyper-masculine patients drew more broad-shouldered claims to see in their patients, with as little basis in reality. 

A bored law student, Tyler Vigen, wrote a program that scrapes the web for datasets with meaningless correlations to show how prevalent they are. The number of murders by steam or hot objects, for example, correlates highly with the age of the reigning Miss America. And the divorce rate in Maine closely tracks the national consumption of margarine.

 

Galton’s family heights data revisited

“Regression” has become the standard term for correlational analyses, but the connection is roundabout. The term initially referred to a specific phenomenon that comes along with correlation, regression to the mean. This ubiquitous but counterintuitive phenomenon was discovered by the Victorian polymath Francis Galton (1822–1911), who plotted the heights of children against the average size of their two parents (the “mid-parent” score, halfway between the mother and the father) in both cases adjusting for the average difference between males and females. He found that “when mid-parents are taller than mediocrity, their children tend to be shorter than they. When mid-parents are shorter than mediocrity, their children tend to be taller than they.” It’s still true, not just of the heights of parents and their children, but of the IQs of parents and their children, and for that matter, of any two variables that are not perfectly correlated. An extreme value in one will tend to be paired with a not-quite-as-extreme value in the other.

This does not mean that tall families are begetting shorter and shorter children and vice versa so that someday all children will line up against the same mark on the wall and the world will have no jockeys or basketball centers. Nor does it mean that the population is converging on a middlebrow IQ of 100, with geniuses and dullards going extinct. People don’t collapse into uniform mediocrity, despite regression to the mean, because the tails of the distribution are constantly being replenished by the occasional very tall child of taller-than-average parents and very short child of shorter-than-average ones.

Regression to the mean is a statistical phenomenon because, in bell-shaped distributions, the more extreme a value is, the less likely it is to turn up. That implies that any other variable is unlikely to live up to its weirdness, or duplicate its winning streak, or suffer from the same run of bad luck, or even the same perfect storm, again, and will backslide toward ordinariness. For height or IQ, the freakish conspiracy would be whatever unusual combination of genes, experiences, and accidents of biology came together in the parents. Many of the components of that combination will be favored in their children, but the combination itself will not be perfectly reproduced. (And vice versa: because regression is a statistical phenomenon, not a causal one, parents regress to their children’s mean, too.)

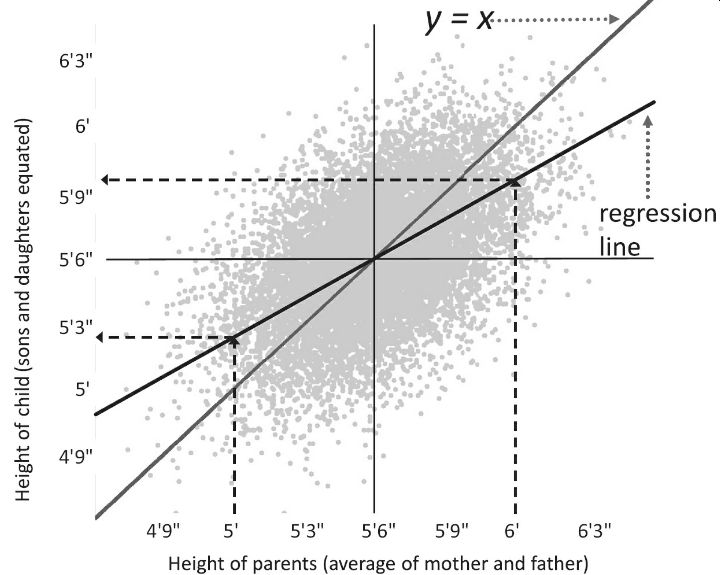
In the above graph, we have a hypothetical dataset similar to Galton’s showing the heights of parents (the average of each couple) and the heights of their adult children (adjusted so that the sons and daughters can be plotted on the same scale). The gray 45-degree diagonal shows what we would expect on average if children were exactly as exceptional as their parents. The black regression line is what we find in reality. If you zero in on an extreme value, say, parents with an average height between them of 6 feet, you’ll find that the cluster of points for their children mostly hangs below the 45-degree diagonal, which you can confirm by scanning up along the right dotted arrow to the regression line, turning left, and following the horizontal dotted arrow to the vertical axis, where it points a bit above 5′9″, shorter than the parents. If you zero in on the parents with an average height of 5 feet (left dotted arrow), you’ll see that their children mostly float above the gray diagonal, and the left turn at the regression line takes you to a value of almost 5′3″, taller than the parents.

Regression to the mean happens whenever two variables are imperfectly correlated, which means that we have a lifetime of experience with it. Nonetheless, Tversky and Kahneman have shown that most people are oblivious to the phenomenon.

Unawareness of regression to the mean sets the stage for many other illusions. After a spree of horrific crimes is splashed across the papers, politicians intervene with SWAT teams, military equipment, Neighborhood Watch signs, and other gimmicks, and sure enough, the following month they congratulate themselves because of the crime rate is not as high. Psychotherapists, too, regardless of their flavor of talking cure, can declare unearned victory after treating a patient who comes in with a bout of severe anxiety or depression. 

Another cause of replication failures is that experimenters don’t appreciate a regression version to the mean called the Winner’s Curse. It’s frequently observed in auctions: The person who bids the most and wins may regret the bid since it often exceeds the value of the auctioned object.

That is if the results of an experiment seem to show an interesting effect, a lot of things must have gone right, whether the effect is real or not. A failure to appreciate how regression to the mean applies to striking discoveries led to a muddled 2010 New Yorker article called “The Truth Wears Off,” which posited a mystical “decline effect,” supposedly casting doubt on the scientific method.

The Winner’s Curse applies to any unusually successful human venture, and our failure to compensate for singular moments of good fortune may be one of the reasons that life so often brings disappointment. 

 

The problem with  causation

Even once we have established that some cause makes a difference to an outcome, neither scientists nor laypeople are content to leave it at that. We connect the cause to its effect with a mechanism: the clockwork behind the scenes that push things around. People have intuitions that the world is not a video game with patterns of pixels giving way to new patterns. Underneath each happening is a hidden force, power, or oomph. Many of our primitive intuitions of causal powers turn out, in the light of science, to be mistaken, such as the “impetus” that the medievals thought was impressed upon moving objects, and the psi, qi, engrams, energy fields, homeopathic miasms, crystal powers, and other bunkum of alternative medicine. But some intuitive mechanisms, like gravity, survive in scientifically respectable forms. And many new hidden mechanisms have been posited to explain correlations in the world, including genes, pathogens, tectonic plates, and elementary particles. These causal mechanisms are what allow us to predict what would happen in counterfactual scenarios, lifting them from the realm of make-believe: we set up the pretend world and then simulate the mechanisms, which take it from there. 

Identifying the cause of an effect raises a thicket of puzzles. When something happens, people commonly ask: What caused that? Making causal judgments is often deceptively easy. We naturally conclude that the lightning strike caused the forest fire, or the scandal caused the political candidate’s defeat. These kinds of causal judgments are also very important, structuring how we understand and interact with our environments.

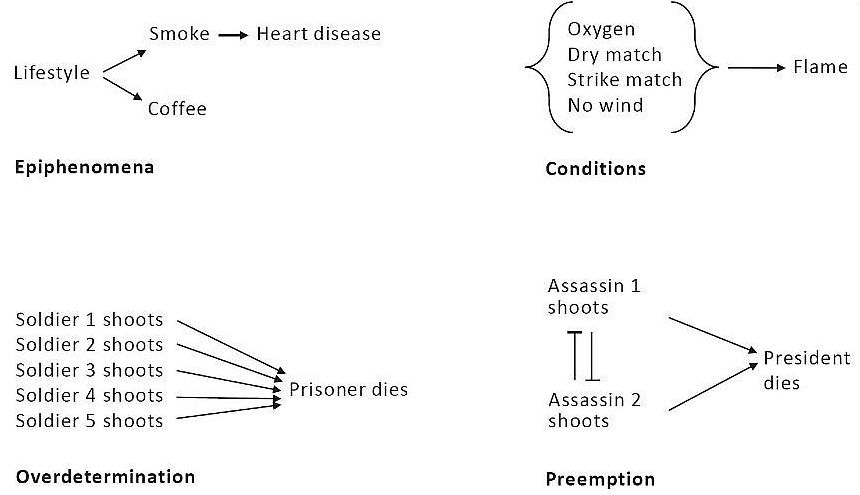
Identifying the cause of an effect is challenging. One difference between a cause and a condition is elusive. We say striking a match causes a fire, but without oxygen, there would be no fire. Why don’t we say “The oxygen caused the fire”?                                                                                   

 

Preemption overdetermination and probabilistic causation

A second puzzle is a preemption. Suppose, for the sake of argument, that Lee Harvey Oswald had a co-conspirator perched on the grassy knoll in Dallas in 1963, and they had conspired that whoever got the first clear shot would take it while the other melted into the crowd. In the counterfactual world in which Oswald did not shoot, JFK would still have died, yet it would be wacky to deny that in the world in which he did take the shot before his accomplice, he caused Kennedy’s death. 

A third is an overdetermination. A condemned prisoner is shot by a firing squad rather than a single executioner so that no shooter has to live with the dreadful burden of being the one who caused the death: if he had not fired, the prisoner would still have died. But then, by the logic of counterfactuals, no one caused his death. 

And then there’s probabilistic causation. Many of us know a nonagenarian who smoked a pack a day all her life. But nowadays few people would say that her ripe old age proves that smoking does not cause cancer, though that was a typical “refutation” in the days before the smoking–cancer link became undeniable. Even today, the confusion between less-than-perfect causation and no causation is rampant. A 2020 New York Times op-ed argued for abolishing the police because “the current approach hasn’t ended [rape]. Most rapists never see the inside of a courtroom.” The editorialist did not consider whether, if there were no police, even fewer rapists, or none at all, would see the inside of a courtroom. 

We can make sense of these paradoxes of causation only by forgetting the billiard balls and recognizing that no event has a single cause. Events are embedded in a network of causes that trigger, enable, inhibit, prevent, and supercharge one another in linked and branching pathways. The four causal puzzlers become less puzzling when we lay out the road maps of causation in each case, shown below.

If you interpret the arrows not as logical implications (“If X smokes, then X gets heart disease”) but as conditional probabilities (“The likelihood of X getting heart disease given that X is a smoker is higher than the likelihood of X getting heart disease given that he is not a smoker”), and the event nodes not as being either on or off but as probabilities, reflecting a base rate or prior, then the diagram is called a causal Bayesian network.

One can work out what unfolds over time by applying (naturally) Bayes’s rule, node by node through the network. No matter how convoluted the tangle of causes, conditions, and confounds, one can then determine which events are causally dependent on or independent of one another:

 

The inventor of these networks, the computer scientist Judea Pearl, notes that they are built out of three simple patterns, the chain, the fork, and the collider, each capturing a fundamental (but unintuitive) feature of causation with more than one cause.

 

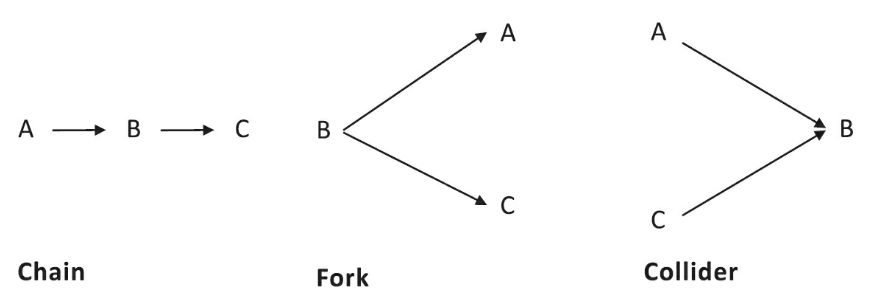
The connections reflect the conditional probabilities. In each case, A and C are not directly connected, which means that the probability of A given B can be specified independently of the probability of C given B. And in each case, something distinctive may be said about the relation between them. 

In a causal chain, the first cause, A, is “screened off” from the ultimate effect, C; its only influence is via B. As far as C is concerned, A might as well not exist. Consider a hotel’s fire alarm, set off by the chain “fire → smoke → alarm.” It’s not a fire alarm but a smoke alarm, indeed, a haze alarm. The guests may be awakened as readily by someone spray-painting a bookshelf near an intake vent as by an errant crème brûlée torch.

A causal fork is already familiar: it depicts a confound or epiphenomenon, with the attendant danger of misidentifying the actual cause. Age affects vocabulary (B) and shoe size (C), since older children have bigger feet and know more words. This means that vocabulary is correlated with shoe size. Head Start should not prepare children for school by fitting them with larger sneakers.

Just as dangerous is the collider, where unrelated causes converge on a single effect. Actually, it’s even more dangerous, because while most people intuitively get the fallacy of a confound (it cracked them up in the shtetl), the “collider stratification selection bias” is almost unknown. The trap in a causal collider is that when you focus on a restricted range of effects, you introduce an artificial negative correlation between the causes since one cause will compensate for the other. Many veterans of the dating scene wonder why good-looking men are jerks. But this may be a calumny on the handsome, and it’s a waste of time to cook up theories to explain it, such as that good-looking men have been spoiled by a lifetime of people kissing up to them. Many women will date a man (B) only if he is either attractive (A) or nice (C). Even if niceness and looks were uncorrelated in the dating pool, the plainer men had to be nice or the woman would never have dated them in the first place, while any such filter did not sort the hunkser. Such a filter introduced a bogus negative correlation that did not sort the critics of standardized testing into thinking that test scores don’t matter, based on the observation that graduate students admitted with higher scores are no more likely to complete the program. The problem is that the students who were accepted despite their low scores must have boasted other assets. If one is unaware of the bias, one could even conclude that maternal smoking is good for babies, since among babies with low birth weights, the ones with mothers who smoked are healthier. That’s because low birth weight must be caused by something, and the other possible causes, such as alcohol or drug abuse, maybe even more harmful to the child. The collider fallacy also explains why Jenny Cavilleri unfairly maintained that rich boys are stupid: to get into Harvard (B), you can be either rich (A) or smart (C).

The problem is that when one thing is correlated with another, it does not necessarily mean that the first caused the second. As the mantra goes: When A is correlated with B, it could mean that A causes B, B causes A, or some third factor, C, causes both A and B. Reverse causation and confounding, the second and third verses of the mantra, are ubiquitous. The world is a substantial causal Bayesian network, with arrows pointing everywhere, entangling events into knots where everything is correlated with everything else. 

 

Causal conclusions

Countries that are richer also tend to be healthier, happier, safer, better educated, less polluted, more peaceful, more democratic, more liberal, more secular, and more gender-egalitarian. People who are richer also tend to be healthier, better educated, better connected, likelier to exercise and eat well, and likelier to belong to privileged groups. These snarls mean that almost any causal conclusion you draw from correlations across countries or across people is likely to be wrong, or at best unproven. Does democracy make a country more peaceful because its leader can’t readily turn citizens into cannon fodder? Or do countries facing no threats from their neighbors have the luxury of indulging in democracy? Does going to college equip you with skills that allow you to earn a good living? Or do only intelligent, disciplined, or privileged people, who can translate their natural assets into financial ones, make it through university? 

There is an impeccable way to cut these knots: the randomized experiment often called a randomized controlled trial or RCT. Take a large sample from the population of interest, randomly divide them into two groups, apply the putative cause to one gro, withhold it from the other, and see if the first group changes while the second does not. A random withhold is the closest we can come to creating the counterfactual world that is the acid test for causation. A causal network consists of surgically severing the putative cause from all its incoming influence, setting it to deterrent values and seeing whether the probabilities of the putative effects differ.

Randomness is the key: if the patients who were given the drug signed up earlier, or lived closer to the hospital, or had more interesting symptoms, than the patients who were given the placebo, you’ll never know whether the drug worked. The wisdom of randomized controlled trials is seeping into policy, economics, and education. Recently referred to as Freakonomics they are urging policymakers to test their nostrums in one set of randomly selected villages, classes, or neighborhoods, and compare the results against a control group that is put on a waitlist or given some meaningless make-work program.

The knowledge gained is likely to outperform traditional ways of evaluating policies, like dogma, folklore, conventional wisdom, and HiPPO. Randomized experiments are no panacea since nothing is a panacea. Laboratory scientists snipe at each other as much as correlational data scientists, because even in an experiment you can’t do just one thing. Experimenters may think they have administered treatment only to the experimental group, but other variables may be confounded with it.

The other problem with experimental manipulations, of course, is that the world is not a laboratory. It’s not as if political scientists can flip a coin, impose democracy on some countries and autocracy on others, and wait five years to see which ones go to war. The same practical and ethical problems apply to studies of individuals, as shown in this cartoon. Michael Shaw/The New Yorker Collection/The Cartoon Bank Though not everything can be studied in an experimental trial, social scientists have mustered their ingenuity to find instances in which the world does the randomization for them. These experiments of nature can sometimes allow one to wring causal conclusions out of a correlational universe. One example is the “regression discontinuity.” 

 

Palliatives for the ailments that enfeeble causal inference

And whereby these palliatives are not as good as the charm of random assignment, but often they are the best we can do in a world that was not created for the benefit of scientists. Reverse causation is the easier of the two to rule out, thanks to the iron law that hems in the writers of science fiction and other time-travel plots like Back to the Future: the future cannot affect the past. Suppose you want to test the hypothesis that democracy causes peace, not just vice versa. First, one must avoid the fallacy of all-or-none causation, and get beyond the common but false claim that “democracies never fight each other” (there are plenty of exceptions). The more realistic hypothesis is that countries that are relatively more democratic are less likely to fall into war.

Several research organizations give countries democracy scores from –10 for a full autocracy like North Korea to +10 for a full democracy like Norway. Peace is a bit harder because (fortunately for humanity, but unfortunately for social scientists) shooting wars are uncommon, so most of the entries in the table would be “0.”

Instead, one can estimate war-proneness by the number of “militarized disputes” a country was embroiled in over a year: the saber-rattlings, alerting of forces, shots fired across bows, warplanes sent scrambling, bellicose threats, and border skirmishes. One can convert this from a war score to a peace score (so that more peaceful countries get higher numbers) by subtracting the count from some large number, like the maximum number of disputes ever recorded. Now one can correlate the peace score against the democracy score. By itself, of course, that correlation proves nothing. 

But suppose that each variable is recorded twice, say, a decade apart. If democracy causes peace, then the democracy score at Time 1 should be correlated with the peace score at Time 2. This, too, proves little, because over a decade, the leopard doesn’t change its spots: a peaceful democracy then may be a peaceful as a control one can look to the o over a decade there diagonal: the correlation between democracy (the democracy score) at Time 2 and Peace (the peace score) at Time 1. This correlation captures any reverse causation, together with the confounds that have stayed put over the decade. If the first correlation (past cause with present effect) is stronger than the second (past effect with present cause), it’s a hint that democracy causes peace rather than vice versa. The technique is called cross-lagged panel correlation, “panel” being argot for a dataset containing measurements at several points in time. 

Confounds, too, maybe tamed by clever statistics. You may have read in science news articles of researchers “holding constant” or “statistically controlling for” some confounded or nuisance variable. The simplest way to do that is called matching. The democracy–peace relationship is infested with plenty of confounds, such as prosperity, education, trade, and membership in treaty organizations. Let’s consider one of them, wealth, measured as GDP per capita. Suppose that for every democracy in our sample we found an autocracy that had the same GDP per capita. If we compare the average peace scores of the democracies with their autocracy doppelgangers, we’d have an estimate of the effects of democracy on peace, holding GDP constant. The logic of matching is straightforward, but it requires a large pool of candidates from which to find suitable matches, and the number explodes as more confounds have to be held constant. That can work for an epidemiological study with tens of thousands of participants to choose from, but not for a political study in a world with just 195 countries.

The more general technique is called multiple regression, and it capitalizes on the fact that a confound is never perfectly correlated with a putative cause. The discrepancies between them turn out to be not bothersome noise but telltale information. Here’s how it could work with democracy, peace, and GDP per capita. First, we plot the putative cause, the democracy score, against the nuisance variable (top left graph), one point per country. (The data are fake, made up to illustrate the logic.) One fits the regression line, and turns one attention to the residuals: the vertical distance between each point and the line, corresponding to the discrepancy between how democratic a country would be if income predicted democracy perfectly and how democratic it is in reality. Now we throw away each country’s original democracy score and replace it with the residual: the measure of how democratic it is, controlling for its income. 

 

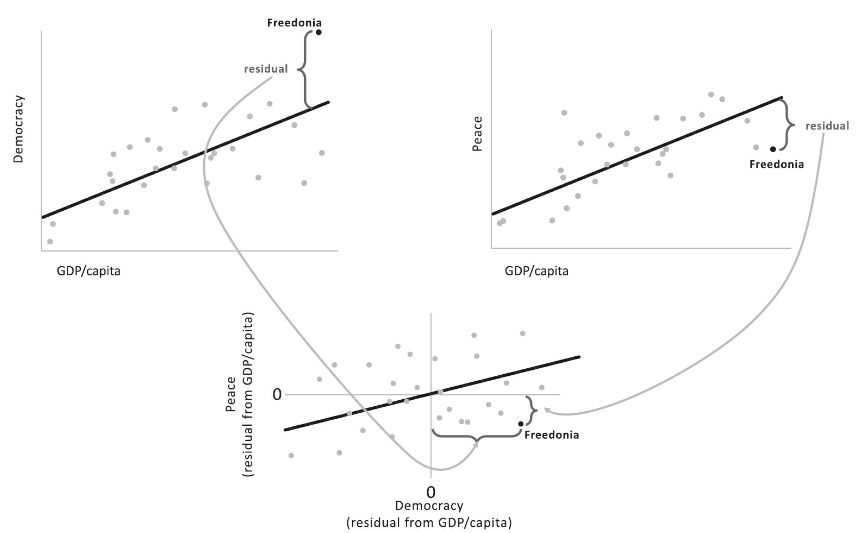
One can do the same with the putative effect, peace. Here one plots the peace score against the nuisance variable (top right graph), measures the residuals, throws away the original peace data, and replaces them with the residuals, namely, how peaceful each country is above and beyond what you would expect from its income. The final step is obvious: correlate the Peace residuals with the Democracy residuals (bottom graph). If the correlation is significantly different from zero, one may venture that democracy causes peacefulness, holding prosperity constant. 

What one has then is the core of the vast majority of statistics used in epidemiology and social sciences, called the general linear model which extends extent the traditional ordinary linear regressors.

The deliverable is an equation that allows one to predict the effect from a weighted sum of the predictors (some of them, presumably, causes). If you’re a good visual thinker, you can imagine the prediction as a tilted plane, rather than a line, floating above the ground defined by the two predictors. Any number of predictors can be thrown in, creating a hyperplane in hyperspace; this quickly overwhelms our feeble powers of visual imagery (which has enough trouble with three dimensions), but in the equation, it consists only of adding more terms to the string. In the case of peace, the equation might be: Peace = (a × Democracy) + (b × GDP/capita) + (c × Trade) + (d × Treaty-membership) + (e × Education), assuming that any of these five might be a pusher or a puller of peacefulness. The regression analysis informs us which of the candidate variables pulls its weight in predicting the outcome, holding each of the others constant. It is not a turnkey machine for proving causation, one still has to interpret the variables and how they are plausibly connected, and watch out for myriad traps, but it is the most commonly used tool for unsnarling multiple causes and confounds. 

 

Adding and Interact

The algebra of a regression equation is less important than the big idea flaunted by its form: events have more than one cause, all of them statistical. The idea seems elementary, but it’s regularly flouted in public discourse. All too often, people write as if every outcome had a single, unfailing cause: if A has been shown to affect B, it proves that C cannot affect it. Accomplished people spend ten thousand hours practicing their craft; this is said to show that achievement is a matter of practice, not talent. Men today cry twice as often as their fathers did; this indicates that the difference in crying between men and women is social rather than biological. The possibility of multiple causes, nature and nurture, talent and practice, is inconceivable. The idea of interacting caus is even more elusivees: the possibility that one cause may depend on another. Everyone benefits from practice, but talented people benefit more. We need a vocabulary for talking and thinking about multiple causes. This is another area in which a few simple concepts from statistics can make everyone smarter. The revelatory concepts are the main effect and interaction. 

Thus suppose one is interested in what makes monkeys fearful: heredity, namely the species they belong to (capuchin or marmoset), or the environment in which they we

-     Heredity.

-     Namely with their mothers or in a large enclosure with parents

-     The other monkey families). 

Suppose we have a way of measuring fear, how closely the monkey approaches a rubber snake. With two

Possible causes and one effect, six diff things can happen. This doesn’t sound very easy, but the possibilities jump off the page as soon as we plot them in graphs. Let’s start with the three simplest ones.

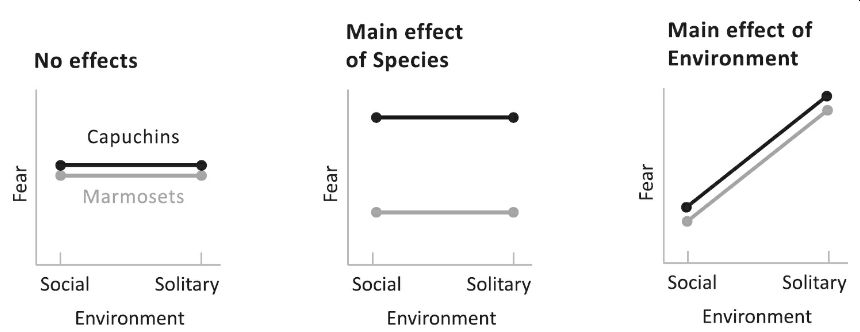
The left graph shows a big fat nothing: a monkey is a monkey. Species doesn’t matter (the lines fall on top of each other); Environment doesn’t matter either (each line is flat). We would see the middle graphene if Species mattered (capuchins are more skittish than marmosets, shown by their line floating higher on the graph). In contrast, environment did not (both species are equally fearful whether they are raised alone or with others, shown by each line being flat). There is a main effect of Species, meaning that the effect is seen across the board, regardless of the Species has the primary impact the opposite outcome. 

We have three possibilities for causes. What would it look like if Species and Environment both mattered: if capuchins were innately more fearful than marmosets and if being reared alone makes a monkey more fearful? The leftmost graph shows this situation, with two main effects. The two lines have parallel slopes. 

 

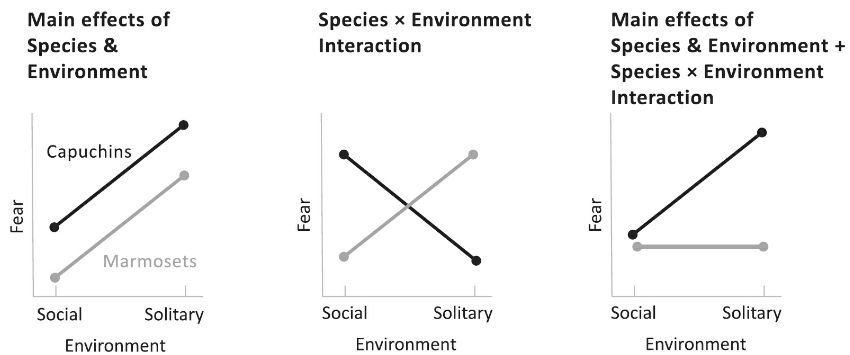
Things get really interesting in the middle graph. Here, both factors matter, but each depends on the other. If you’re a capuchin, being raised alone makes you bolder; if you’re a marmoset, being raised alone makes you meeker. We see an interaction between Species and Environment, which visually consists of the lines being nonparallel. In these data, the lines cross into a perfect X, which means that the main effects are canceled out entiTheoard, Species doesn’t matter: in these data, the midpoint of the capuchin line sits on top of the midpoint of the marmoset line. Environment doesn’t matter across the board either: the average for Social, corresponding to the point midway between the two leftmost tips, lines up with the average for Solitary, corresponding to the point midway between the rightmost ones. Of course Species and Environment do matter: it’s just that how each cause matters depends on the other one. Finally, an interaction can coexist with one or more main effects. In the rightmost graph, being reared alone makes capuchins more fearful, but it has no effect on the always-calm marmosets. Since the effect on the marmosets doesn’t perfectly cancel out the impact on the capuchins, we do see a direct result of Species (the capuchin line is higher) and a primary effect on the environment (the midpoint of the two left dots is lower than the midpoint of the two right ones). But whenever we interpret a phenomenon with two or more causes, any interaction supersedes the main effects: it provides more insight as to what is going on. An interaction usually implies that the two causes intermingle in a single link in the causal chain, rather than taking place in different links and then just adding up. With these data, the common link might be the amygdala, the part of the brain registering fearful experiences, which may be plastic in capuchins but hardwired in marmosets. With these cognitive tools, we are now equipped to make sense of multiple causes in the world: we can get beyond “nature versus nurture” and whether geniuses are “born or made.” Let’s turn to some real data. What causes major depression, a stressful event or a genetic predisposition? This graph plots the likelihood of suffering a major depressive episode in a sample of women with twin sisters.

 

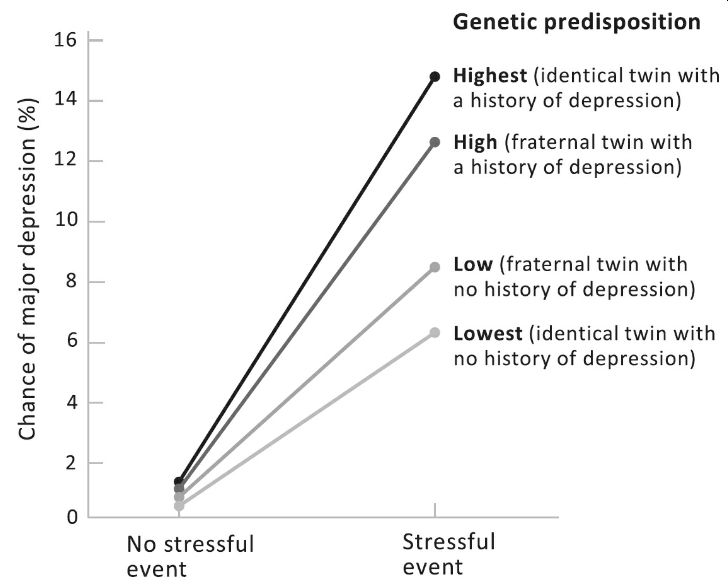
The sample includes women who had undergone a severe stressor, like a divorce, an assault, or a death of a close relative (the points on the right), and women who had not (the points on the left). Scanning the lines from top to bottom, the first is for women who may be highly predisposed to depression, because their identical twin, with whom they share all their genes, suffered from it. The following line down is for women who are only somewhat predisposed to depression, because a fraternal twin, with whom they share half their genes, suffered from it. Below it we have a line for women who are not particularly predisposed, because their fraternal twin did not suffer from depression. At the bottom we find a line for women who are at the lowest risk, because their identical twin did not suffer from it. The pattern in the graph tells us three things. Experience matters: we see a main effect of Stress in the upward slant of the fan of lines, which shows that undergoing a stressful event ups the odds of getting depressed. Overall, genes matter: the four lines float at different heights, indicating that the higher one’s genetic predisposition, the greater the chance that one will suffer a depressive episode. But the real takeaway is the interaction: the lines are not parallel. (Another way of putting it is that the points fall on top of one another on the left but are spread out on the right.) If you don’t suffer a stressful event, your genes barely matter: regardless of your genome, the chance of a depressive episode is less than one percent. But if you do suffer a stressful event, your genes matter a lot: a full dose of genes associated with escaping depression keeps the risk of getting depressed at 6 percent (lowest line); a total amount of the genes related to suffering depression more than doubles the risk to 14 percent (highest line). The interaction tells us that both genes and environment are essential and that they seem to have their effects on the sin the causal chain. 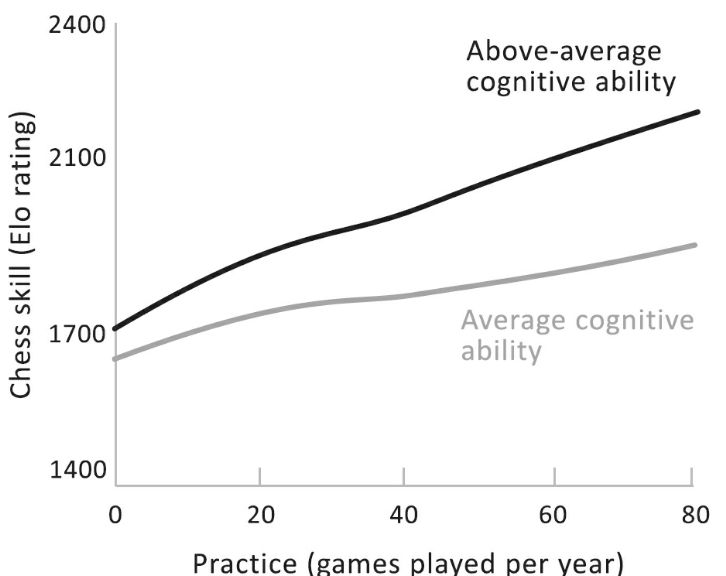These twins' genes and to different degrees are not genes for depression per se; they are genes for vulnerability or resilience to stressful experiences. Let’s turn to whether stars are born or made. The graph on the next page, also from an actual study, shows ratings of chess skill in a sample of lifelong players who differ in their measured cognitive ability and in how many games they play per year. It shows that practice makes better, if not perfect: we see a main effect of games played per year, visible in the overall upward slope. Talent will tell: we see a main effect of ability, visible in the gap between the two lines. But the real moral of the story is their interaction: the lines are not parallel, showing that smarter players gain more with every additional game of practice. An equivalent way of putting it is that without practice, cognitive ability barely matters (the leftmost tips of the lines almost overlap), but with practice, smarter players show off their talent (the rightmost tips are spread apart). Knowing the difference between main effects and interactions not only protects us from falling for false dichotomies but offers us deeper insight into the nature of the underlying causes.

 

Causal Networks and Human Beings As a way of understanding the causal richness of the world, a regression equation is pretty simpleminded: it just adds up a bunch of weighted predictors. Interactions can be thrown in as well; they can be represented as additional predictors derived by multiplying together the interacting ones. 

Yet despite their simplicity, one of the surprising findings of twentieth-century psychology is that a dumb regression equation usually outperforms a human expert. The finding, first noted by the psychologist Paul Meehl, goes by the name “clinical versus actuarial judgment.” Suppose you want to predict some quantifiable outcome, how long a cancer patient will survive; whether a psychiatric patient ends up diagnosed with a mild neurosis or a severe psychosis; whether a criminal defendant will skip bail, blow off parole, or recidivate; how well a student will perform in graduate school; whether a business will succeed or go belly-up; how large a return a stock fund will deliver. You have a set of predictors: a symptom checklist, a group of demographic features, a tally of past behavior, a transcript of undergraduate grades or test scores, anything that might be relevant to the prediction challenge. Now you show the data to an expert, a psychiatrist, a judge, an investment analyst, and so on, and at the same time feed them into a standard regression analysis to get the prediction equation.

Who is the more accurate prognosticator, the expert or the equation? The winner, almost every time, is the equation. An expert who is given the equation and allowed to use it to supplement their judgment often does worse than the equation alone. The reason is that experts are too quick to see extenuating circumstances that they think render the formula inapplicable. It’s sometimes called the broken-leg problem, from the idea that a human expert, but not an algorithm, has the sense to know that a guy who has just broken his leg will not go dancing that evening, even if a formula predicts that he does it every week. The problem is that the equation already considers the likelihood that extenuating circumstances will change the outcome and factors them into the mix with all the other influences. At the same time, the human expert is far too impressed with the eye-catching particulars and too quick to throw the base rates out the window. Indeed, some of the predictors that human experts rely on the most, such as face-to-face interviews, are revealed by regression analyses to be perfectly useless. It’s not that humans can be taken out of the loop. A person still is indispensable in supplying predictors that require real comprehension, like understanding language and categorizing behavior. It’s just that a human is inept at combining them, whereas that is a regression algorithm’s stock in trade. As Meehl notes, at a supermarket checkout counter, you wouldn’t say to the cashier, “It looks to me like the total is around $76; is that OK?” Yet, that is what we do when we intuitively combine a set of probabilistic causes. For all the power of a regression equation, the most humbling discovery about predicting human behavior is how unpredictable it is. It’s easy to say that a combination of heredity and environment causes behavior. Yet when we look at a predictor that has to be more potent than the best regression equation, a person’s identical twin, who shares her genome, family, neighborhood, schooling, and culture, we see that the correlation between the two twins’ traits, while way higher than chance, is way lower than 1, typically around.6

That leaves a lot of human differences mysteriously unexplained: despite near-identical causes, the effects are nowhere near identical. One twin may be gay and the other straight, one schizophrenic and the other functioning normally. In the depression graph, we saw that the chance that a woman will suffer depression if she is hit with a stressful event and has a proven genetic disposition to depression is not 100 percent but only 14 percent. A recent lollapalooza of a study reinforces the cussed unpredictability of the human species. One hundred sixty teams of researchers were given a massive dataset on thousands of fragile families, including their income, education, health records, and the results of multiple interviews and in-home assessments. The teams were challenged to predict the families’ outcomes, such as the children’s grades and the parents’ likelihood of being evicted, employed, or signed up for job training. The competitors were allowed to sic whichever algorithm they wanted on the problem: regression, deep learning, or any other fad or fashion in artificial intelligence. The results? In the understated words of the paper abstract: “The best predictions were not very accurate.” Idiosyncratic traits of each family swamped the generic predictors, no matter how cleverly they were combined. It’s a reassurance to people who worry that artificial intelligence will soon predict our every move. But it’s also a chastening smackdown of our pretensions to fully understand the causal network in which we find ourselves. 

 

For updates click homepage here